Line search

1 Problem

Suppose, we have a problem of minimization of a function f(x): \mathbb{R} \to \mathbb{R} of scalar variable:

f(x) \to \min_{x \in \mathbb{R}}

Sometimes, we refer to the similar problem of finding minimum on the line segment [a,b]:

f(x) \to \min_{x \in [a,b]}

Line search is one of the simplest formal optimization problems, however, it is an important link in solving more complex tasks, so it is very important to solve it effectively. Let’s restrict the class of problems under consideration where f(x) is a unimodal function.

Function f(x) is called unimodal on [a, b], if there is x_* \in [a, b], that f(x_1) > f(x_2) \;\;\; \forall a \le x_1 < x_2 < x_* and f(x_1) < f(x_2) \;\;\; \forall x_* < x_1 < x_2 \leq b

Illustration

2 Key property of unimodal functions

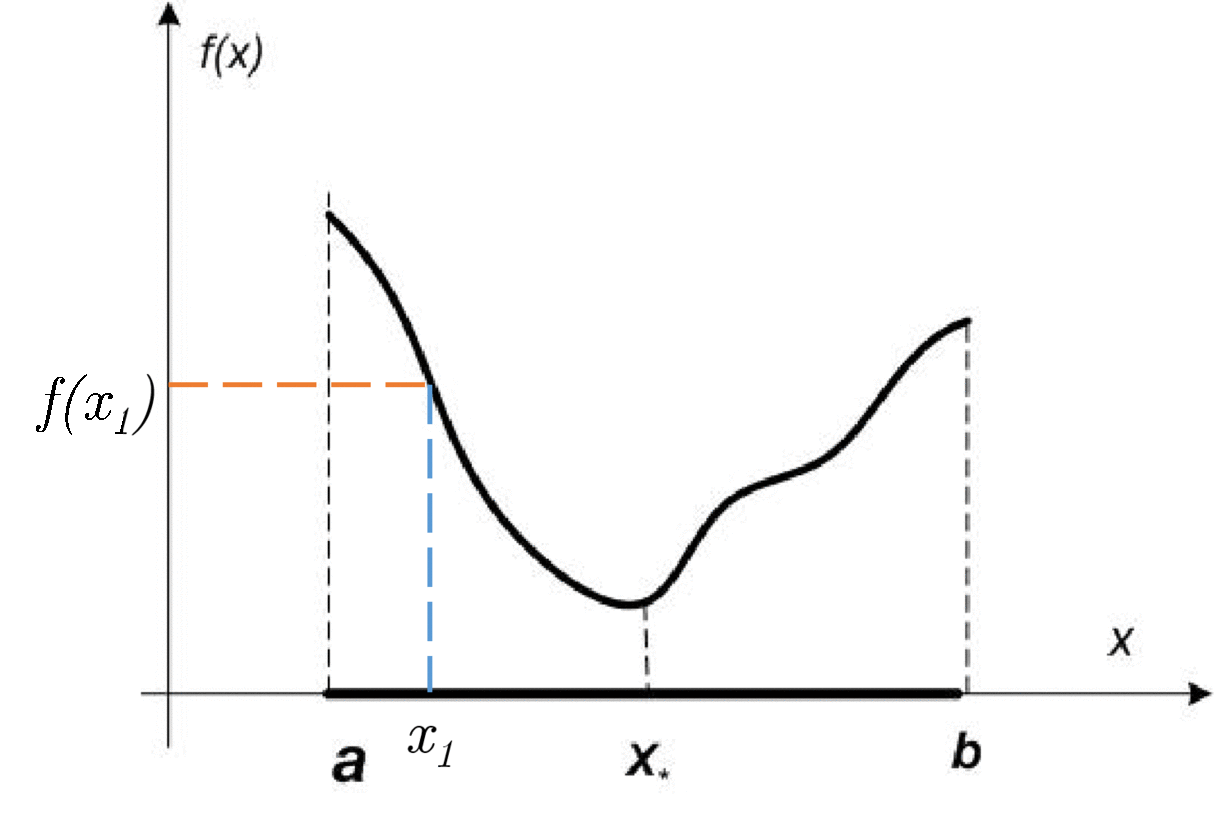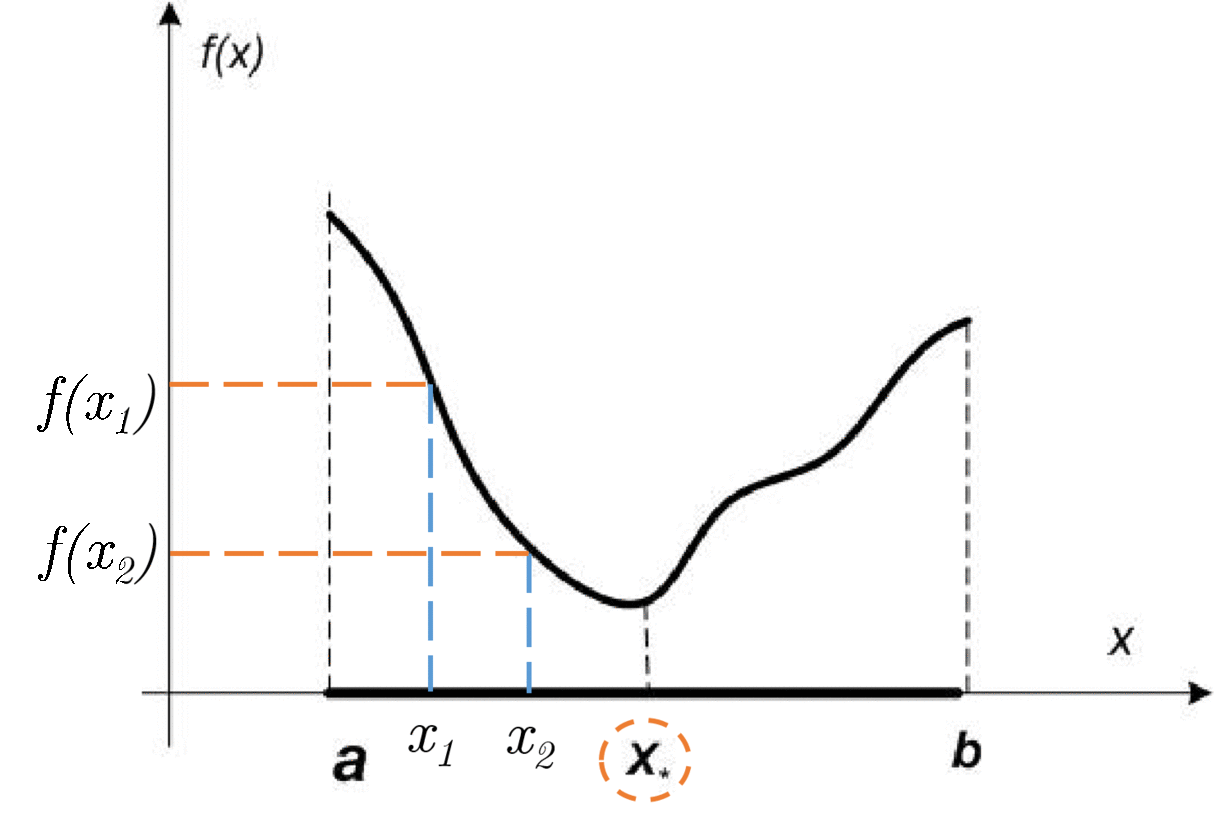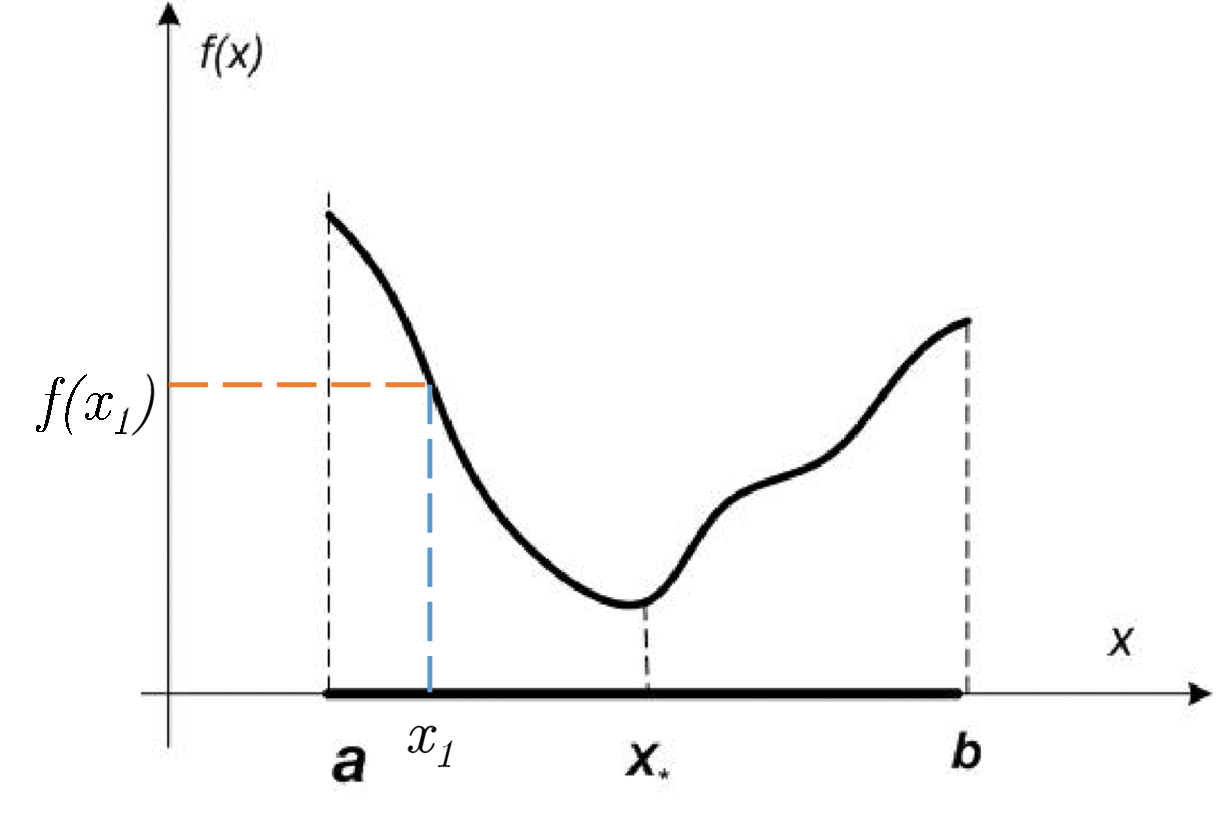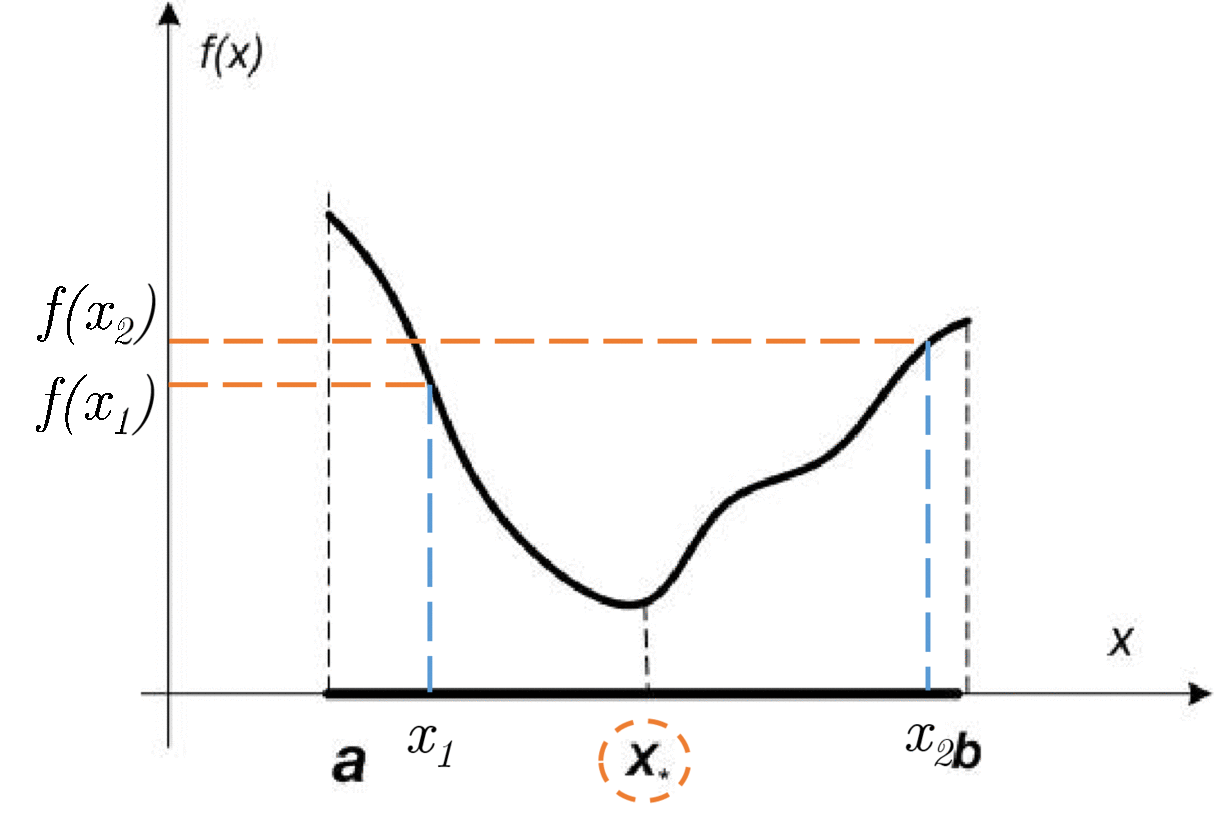
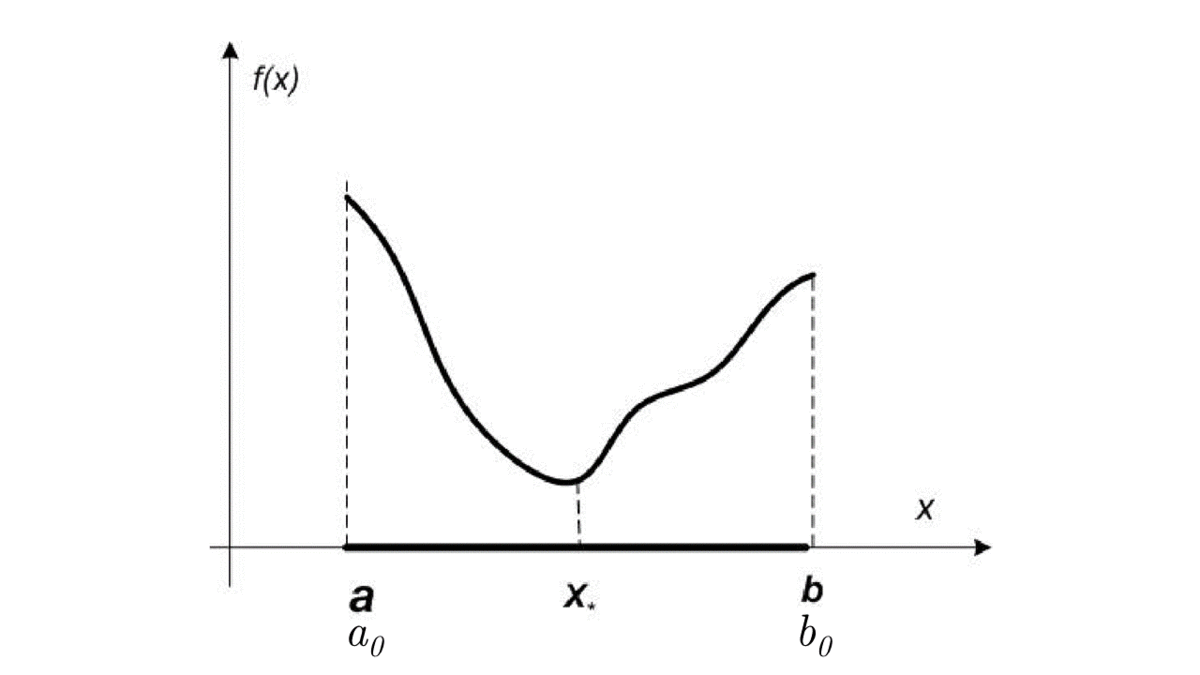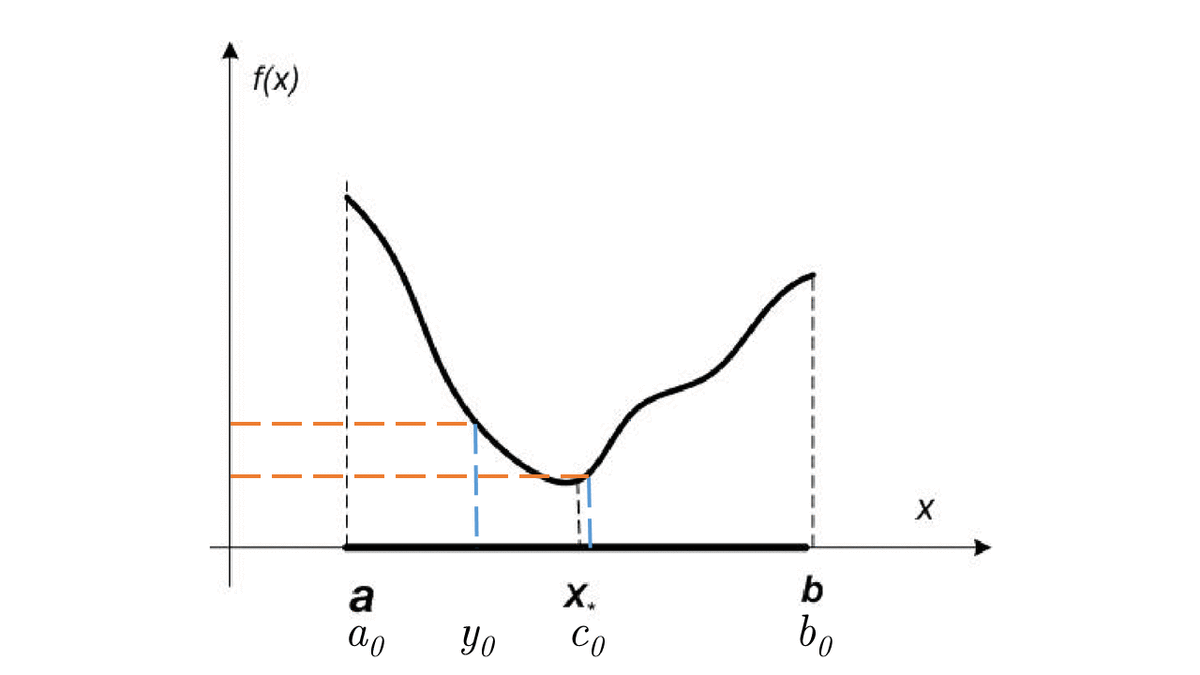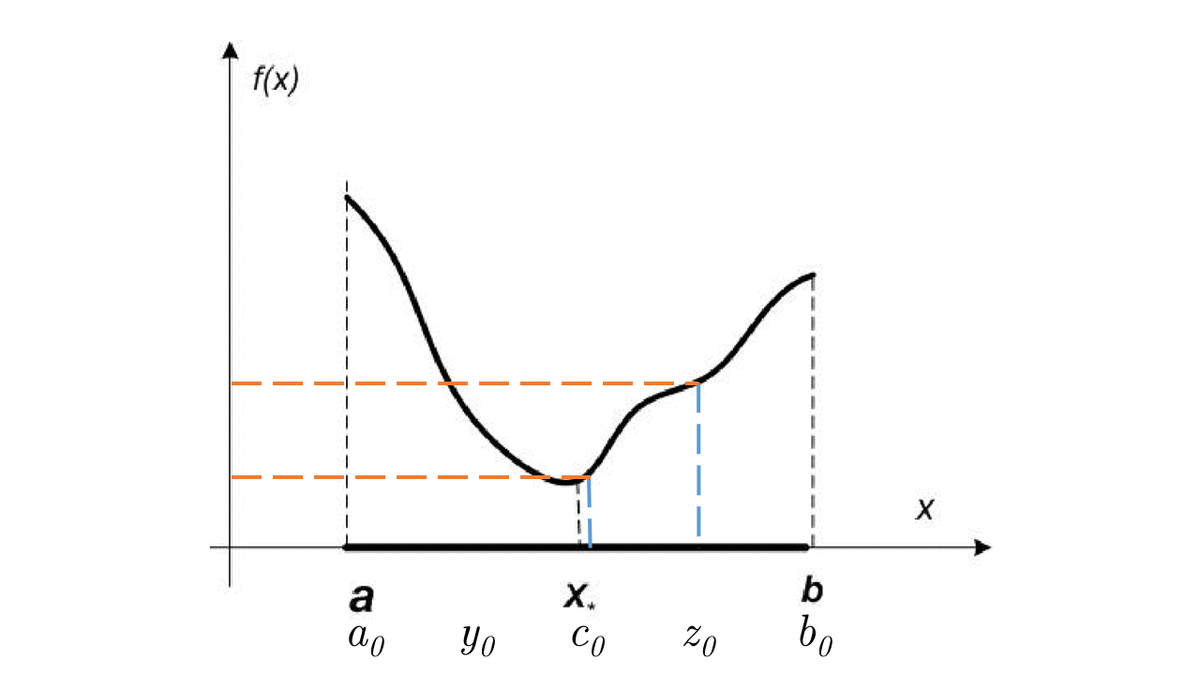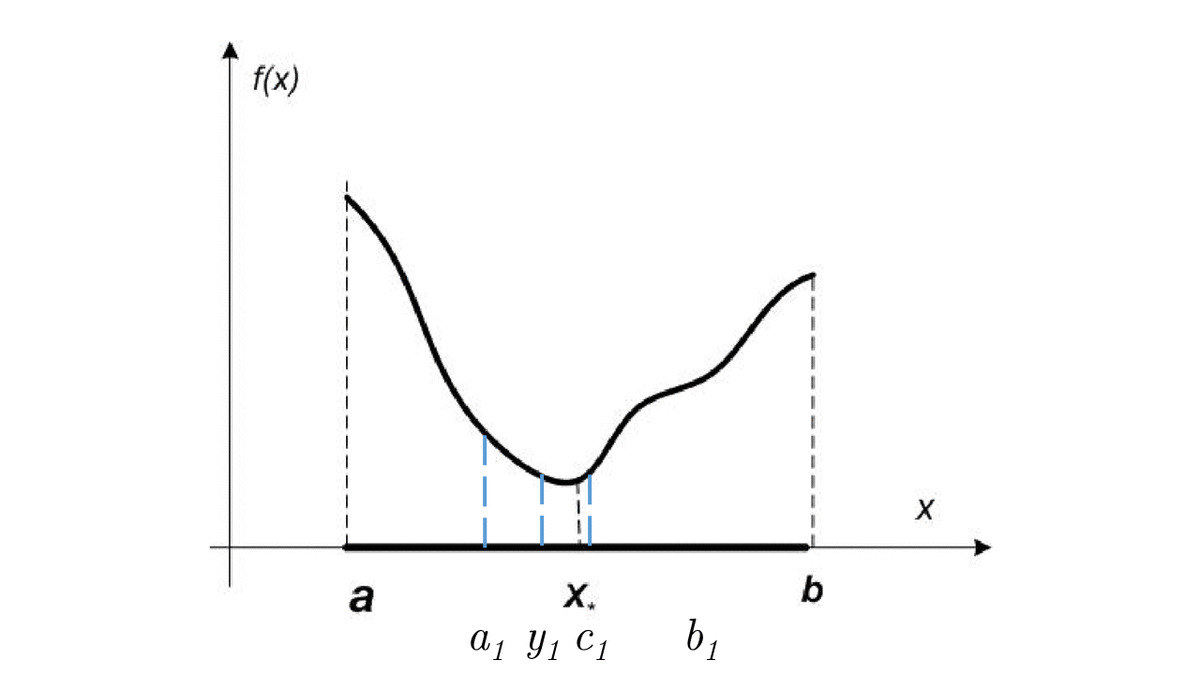
Let f(x) be unimodal function on [a, b]. Than if x_1 < x_2 \in [a, b], then:

  • if f(x_1) \leq f(x_2) \to x_* \in [a, x_2]
  • if f(x_1) \geq f(x_2) \to x_* \in [x_1, b] Illustration

3 Code

Open In Colab

4 References