Newton method

1 Intuition

1.1 Newton’s method to find the equation’ roots

Consider the function \varphi(x): \mathbb{R} \to \mathbb{R}. Let there be equation \varphi(x^*) = 0. Consider a linear approximation of the function \varphi(x) near the solution (x^* - x = \Delta x):

\varphi(x^*) = \varphi(x + \Delta x) \approx \varphi(x) + \varphi'(x)\Delta x.

We get an approximate equation:

\varphi(x) + \varphi'(x) \Delta x = 0

We can assume that the solution to equation \Delta x = - \dfrac{\varphi(x)}{\varphi'(x)} will be close to the optimal \Delta x^* = x^* - x.

We get an iterative scheme:

x_{k+1} = x_k - \dfrac{\varphi(x_k)}{\varphi'(x_k)}.

Illustration

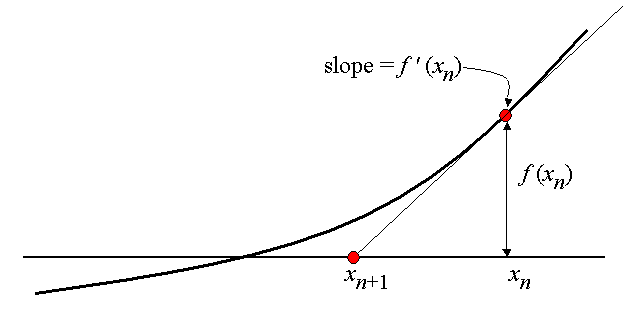
This reasoning can be applied to the unconditional minimization task of the f(x) function by writing down the necessary extremum condition:

f'(x^*) = 0

Here \varphi(x) = f'(x), \; \varphi'(x) = f''(x). Thus, we get the Newton optimization method in its classic form:

\tag{Newton} x_{k+1} = x_k - \left[ f''(x_k)\right]^{-1}f'(x_k).

With the only clarification that in the multidimensional case: x \in \mathbb{R}^n, \; f'(x) = \nabla f(x) \in \mathbb{R}^n, \; f''(x) = \nabla^2 f(x) \in \mathbb{R}^{n \times n}.

1.2 Second order Taylor approximation of the function

Let us now give us the function f(x) and a certain point x_k. Let us consider the square approximation of this function near x_k:

\tilde{f}(x) = f(x_k) + \langle f'(x_k), x - x_k\rangle + \frac{1}{2} \langle f''(x_k)(x-x_k), x-x_k \rangle.

The idea of the method is to find the point x_{k+1}, that minimizes the function \tilde{f}(x), i.e. \nabla \tilde{f}(x_{k+1}) = 0.

Illustration

\begin{align*} \nabla \tilde{f}(x_{k+1}) &= f'(x_{k}) + f''(x_{k})(x_{k+1} - x_k) = 0 \\ f''(x_{k})(x_{k+1} - x_k) &= -f'(x_{k}) \\ \left[ f''(x_k)\right]^{-1} f''(x_{k})(x_{k+1} - x_k) &= -\left[ f''(x_k)\right]^{-1} f'(x_{k}) \\ x_{k+1} &= x_k -\left[ f''(x_k)\right]^{-1} f'(x_{k}). \end{align*}

Let us immediately note the limitations related to the necessity of the Hessian’s non-degeneracy (for the method to exist), as well as its positive definiteness (for the convergence guarantee).

Quadratic approximation and Newton step (in green) for varying starting points (in red). Note that when the starting point is far from the global minimizer (in 0), the Newton step totally overshoots the global minimizer. Picture was taken from the post.

2 Convergence

Let’s try to get an estimate of how quickly the classical Newton method converges. We will try to enter the necessary data and constants as needed in the conclusion (to illustrate the methodology of obtaining such estimates).

\begin{align*} x_{k+1} - x^* = x_k -\left[ f''(x_k)\right]^{-1} f'(x_{k}) - x^* = x_k - x^* -\left[ f''(x_k)\right]^{-1} f'(x_{k}) = \\ = x_k - x^* - \left[ f''(x_k)\right]^{-1} \int_0^1 f''(x^* + \tau (x_k - x^*)) (x_k - x^*) d\tau = \\ = \left( 1 - \left[ f''(x_k)\right]^{-1} \int_0^1 f''(x^* + \tau (x_k - x^*)) d \tau\right) (x_k - x^*)= \\ = \left[ f''(x_k)\right]^{-1} \left( f''(x_k) - \int_0^1 f''(x^* + \tau (x_k - x^*)) d \tau\right) (x_k - x^*) = \\ = \left[ f''(x_k)\right]^{-1} \left( \int_0^1 \left( f''(x_k) - f''(x^* + \tau (x_k - x^*)) d \tau\right)\right) (x_k - x^*)= \\ = \left[ f''(x_k)\right]^{-1} G_k (x_k - x^*) \end{align*}

Used here is: G_k = \int_0^1 \left( f''(x_k) - f''(x^* + \tau (x_k - x^*)) d \tau\right). Let’s try to estimate the size of G_k:

\begin{align*} \| G_k\| = \left\| \int_0^1 \left( f''(x_k) - f''(x^* + \tau (x_k - x^*)) d \tau\right)\right\| \leq \\ \leq \int_0^1 \left\| f''(x_k) - f''(x^* + \tau (x_k - x^*)) \right\|d\tau \leq \qquad \text{(Hessian's Lipschitz continuity)}\\ \leq \int_0^1 M\|x_k - x^* - \tau (x_k - x^*)\| d \tau = \int_0^1 M\|x_k - x^*\|(1- \tau)d \tau = \frac{r_k}{2}M, \end{align*}

where r_k = \| x_k - x^* \|.

So, we have:

r_{k+1} \leq \left\|\left[ f''(x_k)\right]^{-1}\right\| \cdot \frac{r_k}{2}M \cdot r_k

Already smells like quadratic convergence. All that remains is to estimate the value of Hessian’s reverse.

Because of Hessian’s Lipschitz continuity and symmetry:

\begin{align*} f''(x_k) - f''(x^*) \succeq - Mr_k I_n \\ f''(x_k) \succeq f''(x^*) - Mr_k I_n \\ f''(x_k) \succeq \mu I_n - Mr_k I_n \\ f''(x_k) \succeq (\mu- Mr_k )I_n \\ \end{align*}

So, (here we should already limit the necessity of being f''(x_k) \succ 0 for such estimations, i.e. r_k < \frac{\mu}{M}).

\begin{align*} \left\|\left[ f''(x_k)\right]^{-1}\right\| \leq (\mu - Mr_k)^{-1} \end{align*}

r_{k+1} \leq \dfrac{r_k^2 M}{2(\mu - Mr_k)}

The convergence condition r_{k+1} < r_k imposes additional conditions on r_k: \;\;\; r_k < \frac{2 \mu}{3M}

Thus, we have an important result: Newton’s method for the function with Lipschitz positive Hessian converges quadratically near (\| x_0 - x^* \| < \frac{2 \mu}{3M}) to the solution.

2.1 Theorem

Let f(x) be a strongly convex twice continuously differentiated function at \mathbb{R}^n, for the second derivative of which inequalities are executed: \mu I_n\preceq f''(x) \preceq L I_n. Then Newton’s method with a constant step locally converges to solving the problem with superlinear speed. If, in addition, Hessian is Lipschitz continuous, then this method converges locally to x^* at a quadratic rate.

3 Summary

It’s nice:

  • quadratic convergence near the solution x^*
  • affinity invariance
  • the parameters have little effect on the convergence rate

It’s not nice:

  • it is necessary to store the hessian on each iteration: \mathcal{O}(n^2) memory
  • it is necessary to solve linear systems: \mathcal{O}(n^3) operations
  • the Hessian can be degenerate at x^*
  • the hessian may not be positively determined \to direction -(f''(x))^{-1}f'(x) may not be a descending direction

3.1 Possible directions

  • Newton’s damped method (adaptive stepsize)
  • Quasi-Newton methods (we don’t calculate the Hessian, we build its estimate - BFGS)
  • Quadratic evaluation of the function by the first order oracle (superlinear convergence)
  • The combination of the Newton method and the gradient descent (interesting direction)
  • Higher order methods (most likely useless)

4 Materials

5 Code

Open In Colab