Mirror descent

Метод зеркального спуска является естественным обобщением метода проекции субградиента в случае обобщения l_2 нормы на более общий случай какой-то функции расстояния.

0.1 Dual norm:

Определение: Сопряженной нормой \|\cdot\|_* к данной \|\cdot\| называется:

\|y\|_* = \max \{\langle y,x\rangle: \|x\|=1 \}

Пример: (\|\cdot \|_p)_* = \|\cdot \|_q, \qquad \dfrac{1}{p} + \dfrac{1}{q} = 1

Доказательство:

Неравенство Гельдера:

\sum_{k=1}^n |x_k\,y_k| \le \biggl( \sum_{k=1}^n |x_k|^p \biggr)^{\frac{1}{p}} \biggl( \sum_{k=1}^n |y_k|^q \biggr)^{\frac{1}{q}} \text{ for all }x, y \in \mathbb{C}^n

Свойства:

Двойственная норма \|\cdot\|_* является нормой
l_2 норма сопряжена сама себе
Двойственная норма к двойственной норме - исходная норма
(\|\cdot\|_1)_* = \|\cdot\|_\infty, \;(\|\cdot\|_\infty)_* = \|\cdot\|_1
Обобщенное неравенство Коши Шварца: \langle y,x \rangle \leq \|y\|_*\|x\|, следствие: \|x\|^2 \pm 2 \langle y,x \rangle + \|y\|_*^2 \geq 0

0.2 Bregman divergence

Попробуем интуитивно ввести понятие обобщенного расстояния, именуемого расстоянием Брэгмана. Для каждой точки y она возвращает расстояние этой точки до x - V_x(y). В самом простом случае можно взять V_x(y) = \frac{1}{2}\|x-y\|^2, \;\; \nabla V_x(y) = y-x. Рассмотрим уже классическую запись:

\begin{align*} \|x_{k+1} - y\|^2 &= \|x_{k+1}-x_k \|^2 + \|x_k - y\|^2 - 2 \langle x_k - x_{k+1} ,x_k - y\rangle \\ \tag{Req1} V_{x_{k+1}}(y) &= V_{x_{k+1}}(x_k) + V_{x_{k}}(y) - \langle \nabla V_{x_{k+1}(x_k)}, x_k - y \rangle \end{align*}

Для вводимого обобщенного расстояния будем требовать выполнения (Req1), кроме того (как будет видно при получении оценок), приятным свойством было бы еще следующее требование:

\tag{Req2} V_x(y) \geq \frac{1}{2} \|x-y\|^2

Определение: Дивергенцией (расстоянием) Брэгмана называется функция следующая V_x(y). Пусть S \subseteq \mathbb{R}^n - замкнутое выпуклое множество, тогда функция \phi : S \to \mathbb{R} называется прокс-функцией (distance generating function), если \phi является 1 - сильно выпуклой, т.е.:

\phi(y) \geq \phi(x) + \langle \nabla \phi(x), y-x\rangle + \frac{1}{2} \|y-x\|^2, \qquad \forall x,y \in S

Тогда прокс-функцией индуцируется расстояние Брэгмана:

V_x(y) = \phi(y) - \phi(x) - \langle\nabla \phi(x), y-x\rangle

Заметим, что определение сильной выпуклости зависит от выбора прямой нормы \|\cdot\|. Это важное замечание, поскольку именно это свойство позволит в будущем подстраивать расстояние под геометрию пространства.

0.2.1 Examples

Выберем норму в прямом пространстве \|\cdot\| = \|\cdot\|_2, пусть \phi(x) = \frac{1}{2}\|x\|^2, тогда расстояние Брэгмана V_x(y) = \frac{1}{2}\|x-y\|^2. Такой выбор совпадает с тем, что мы видели ранее в методе проекции субградиента
Выберем теперь другую норму \|\cdot\| = \| \cdot \|_1, пусть \phi(x) = \sum\limits_{i \in [n]}x_i \log x_i - антиэнтропия. Тогда эта функция будет 1 сильно выпукла на выпуклом множестве S : \left\{x \in S : x \geq 0, \sum\limits_{i \in [n]} x_i = 1\right\} (вероятностном симплексе), а соответствующая ей дивергенция Брэгмана: V_x(y) = \sum\limits_{i \in [n]} y_i \log \frac{y_i}{x_i} = D(y \| x) - расстояние Кульбака - Ляйблера.
Еще немного примеров отсюда:

0.2.2 Свойства

Аксиома тождества V_x(x) = 0
Совместимость с Евклидовой нормой: V_x(y) \geq \frac{1}{2}\|x-y\|^2 \geq 0
(Не)равенство треугольника: \langle -\nabla V_x(y), y-z\rangle = V_x(z) - V_y(z) - V_x(y)

Первые два свойства очевидны из определения. Докажем третье:

\begin{align*} \langle -\nabla V_x(y), y-z\rangle &= \langle \nabla \phi(x) - \nabla \phi(y) , y-z\rangle =\\ & = (\phi(z) - \phi(x) - \langle \nabla \phi(x), z -x \rangle) \\ & - (\phi(z) - \phi(y) - \langle \nabla \phi(y), z - y \rangle) \\ & - (\phi(y) - \phi(x) - \langle \nabla \phi(x), y - x \rangle) \\ & = V_x(z) - V_y(z) - V_x(y) \end{align*}

1 Возвращение к истокам

Пусть задано выпуклое замкнутое множество S \in \mathbb{R}^n, кроме того, есть алгоритм оптимизации, возвращающий последовательность точек x_1, \ldots, x_k, \ldots. Тогда запишем (не)равенство треугольника для расстояния Брэгмана, полагая y = x_{k+1}, x = x_k и произвольный z \in S (который мы в дальнейшем для целостности изложения будем обозначать y)

\begin{align*} \langle -\nabla V_{x_k}(x_{k+1}), x_{k+1}-z\rangle &= V_{x_k}(z) - V_{x_{k+1}}(z) - V_{x_k}(x_{k+1}) \\ \tag{baseMD} \langle -\nabla V_{x_k}(x_{k+1}), x_{k+1}-y\rangle &= V_{x_k}(y) - V_{x_{k+1}}(y) - V_{x_k}(x_{k+1}) \end{align*}

Просуммируем полученные равенства:

\sum\limits_{k = 0}^{T-1}\langle -\nabla V_{x_k}(x_{k+1}), x_{k+1}-y\rangle = V_{x_0}(y) - V_{x_{T}}(y) - \sum\limits_{k = 0}^{T-1}V_{x_k}(x_{k+1})

Имея ввиду полученное уравнение, давайте, наконец, попробуем сформулировать метод зеркального спуска:

x_{k+1} = \text{arg}\min\limits_{x \in S} \left( \langle \alpha_k g_k, x \rangle + V_{x_k}(x) \right)

Посмотрим внимательнее на условие проекции для точки x_{k+1}:

\langle \alpha_k g_k,x_{k+1} - y\rangle + \langle \nabla V_{x_k}(x_{k+1}),x_{k+1} - y\rangle \leq 0

\langle \alpha_k g_k,x_{k+1} - y\rangle \leq - \langle \nabla V_{x_k}(x_{k+1}),x_{k+1} - y\rangle

Попробуем теперь получить наше базовое неравенство, используя (baseMD):

\begin{align*} \langle \alpha_k g_k, x_k - y\rangle &\leq - \langle \nabla V_{x_k}(x_{k+1}),x_{k+1} - y\rangle - \langle \alpha_k g_k, x_{k+1} - x_k\rangle = \\ & = V_{x_k}(y) - V_{x_{k+1}}(y) - V_{x_k}(x_{k+1})- \langle \alpha_k g_k, x_{k+1} - x_k\rangle \leq\\ &\leq V_{x_k}(y) - V_{x_{k+1}}(y) - \frac{1}{2}\|x_k - x_{k+1}\|^2- \langle \alpha_k g_k, x_{k+1} - x_k\rangle \leq \\ &\leq V_{x_k}(y) - V_{x_{k+1}}(y) + \left(\langle \alpha_k g_k, x_k - x_{k+1}\rangle- \frac{1}{2}\|x_k - x_{k+1}\|^2 \right) \leq \\ &\leq V_{x_k}(y) - V_{x_{k+1}}(y) + \frac{\alpha_k^2}{2} \|g_k\|_*^2 \end{align*}

ТЕЛЕСКОПИРУЕМ

\begin{align*} \sum\limits_{k = 0}^{T-1} \langle \alpha_k g_k, x_k - y\rangle &\leq V_{x_0}(y) - V_{x_{T}}(y) + \sum\limits_{k = 0}^{T-1}\frac{\alpha_k^2}{2} \|g_k\|_*^2 \\ &\leq V_{x_0}(y) + \sum\limits_{k = 0}^{T-1}\frac{\alpha_k^2}{2} \|g_k\|_*^2 \\ &\leq M + \dfrac{\alpha^2 G^2 T}{2} \end{align*}

Здесь мы подразумеваем \|g_k\|_* \leq G равномерно по k, а V_{x_0}(y) \leq M. В итоге:

\begin{align*} f(\overline{x}) - f^* &= f \left( \frac{1}{T}\sum\limits_{k=0}^{T-1} x_k \right) - f^* \leq \dfrac{1}{T} \left( \sum\limits_{k=0}^{T-1} f(x_k) - f^* \right) \\ & \leq \dfrac{1}{T} \left( \sum\limits_{k=0}^{T-1}\langle g_k, x_k - x^* \rangle\right) \\ & \leq \dfrac{M}{\alpha T} + \dfrac{\alpha G^2}{2} \leq \sqrt{\dfrac{2 M G^2}{T}} \end{align*}

Выбирая шаг \alpha_k = \alpha = \sqrt{\dfrac{2M}{G^2 T}}

1.1 Алгоритм зеркального спуска (mirror descent):

x_{k+1} = \text{arg}\min\limits_{x \in S} \left( \langle \alpha_k g_k, x \rangle + V_{x_k}(x) \right)

Интересные фишки:

Такая же скорость сходимости, как и для метода проекции субградиента.
Работает в существенно более широком классе практических задач

1.2 Онлайн версия

Совершенно ясно, что в наших оценках на каждом шаге может быть новая функция f_k(x) на заданном классе. Поэтому, аналогичные оценки получаются и для онлайн постановки:

R_{T-1} = \sum\limits_{k = 0}^{T-1} f_k(x_k) - \min_{x} \sum\limits_{k = 0}^{T-1} f_k(x) \leq \sqrt{2 M G^2 T}

\overline{R_{T-1}} = \dfrac{1}{T}R_{T-1} \leq \sqrt{\dfrac{2 M G^2}{T}}

1.3 Еще одна интерпретация

Давайте покажем, что полученный алгоритм имеет еще одну очень интуитивную интерпретацию:

y_{k} = \nabla \phi(x_k) Отображение в сопряженное пространство с помощью функции \nabla \phi(x)
y_{k+1} = y_k - \alpha_k \nabla f_k(x_k) Градиентный шаг в сопряженном пространстве
x_{k+1} = \text{arg}\min\limits_{x \in S}V_{\nabla \phi^*(y_{k+1})}(x) Обратное отображение с помощью функции \nabla \phi^*(x) и проекция на бюджетное множество

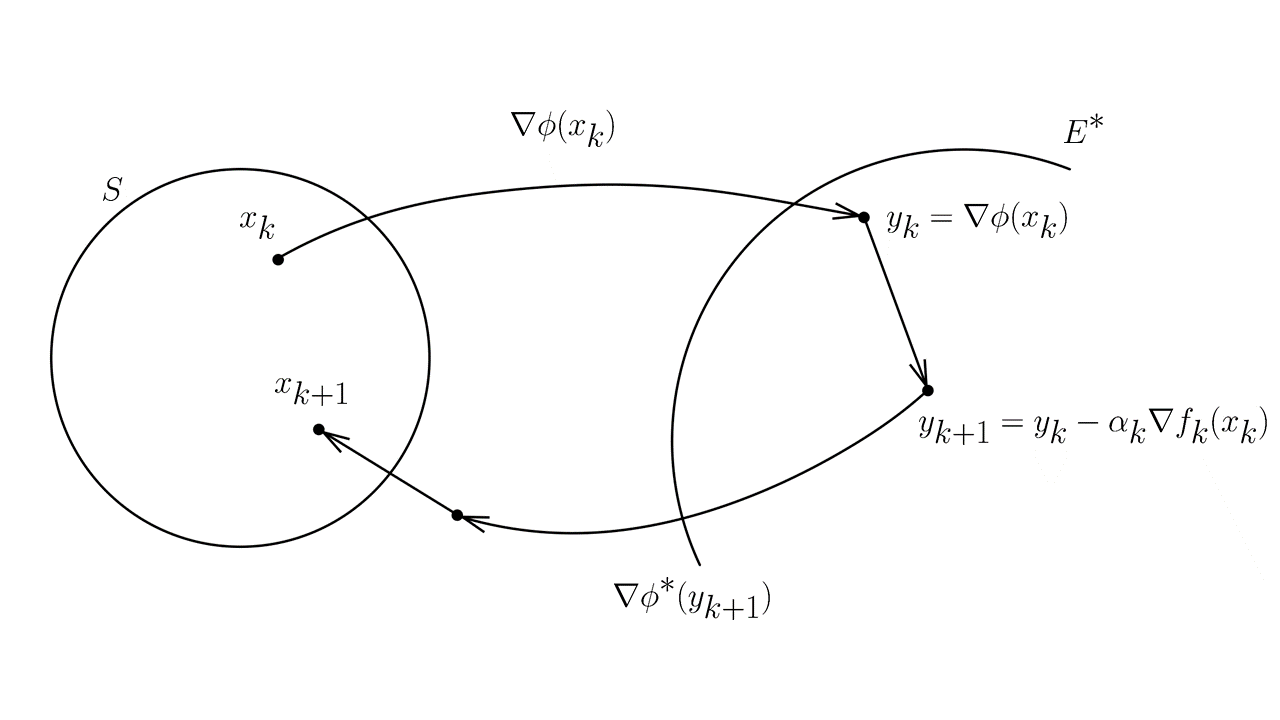
Для доказательства эквивалентности таких записей, следует сначала доказать факт того, что:

\left( \nabla \phi(x) \right)^{-1} = \nabla \phi^*(y)

Для этого пусть y = \nabla \phi(x). Заметим, что для сопряженной функции справедливо неравенство Фенхеля - Юнга: \phi^*(y) + \phi(x) \geq xy, в случае, если \phi(x) - дифференцируема, такое преобразование называется преобразованием Лежандра и выполняется равенство: \phi^*(y) + \phi(x) = xy. Дифференцируя равенство по y, получаем \nabla \phi^*(y) = x. Таким образом,

\nabla\phi^*(y) = \nabla\phi^*(\nabla \phi(x)) = x, \qquad \nabla\phi(x) = \nabla\phi(\nabla \phi^*(y)) = y

Доказательство:

\begin{align*} x_{k+1} &= \text{arg}\min\limits_{x \in S} \left\{ V_{\nabla \phi^*(y_{k+1})}(x) \right\} = \\ &= \text{arg}\min\limits_{x \in S} \left\{ \phi(x) - \phi(\nabla \phi^*(y_{k+1})) - \left\langle \nabla \phi (\nabla \phi^*(y_{k+1})),x - \nabla \phi^*(y_{k+1})\right\rangle\right\} = \\ &= \text{arg}\min\limits_{x \in S} \left\{ \phi(x) - \left\langle y_{k+1},x \right\rangle \right\} = \\ &= \text{arg}\min\limits_{x \in S} \left\{ \phi(x) - \left\langle \nabla \phi(x_k) - \alpha_k g_k,x \right\rangle \right\} = \\ &= \text{arg}\min\limits_{x \in S} \left\{ \phi(x) - \phi(x_k) - \left\langle \nabla \phi(x_k),x \right\rangle + \left\langle \alpha_k g_k,x \right\rangle \right\} = \\ &= \text{arg}\min\limits_{x \in S} \left\{ V_{x_k}(x) + \left\langle \alpha_k g_k,x \right\rangle \right\} \end{align*}

В последней строчке мы пришли к той формулировке, которую писали раньше. Заметим так же, еще одну интересную концепцию:

\begin{align*} x_{k+1} &= \text{arg}\min\limits_{x \in S} \left( \langle \alpha_k g_k, x \rangle + V_{x_k}(x) \right) \\ &= \text{arg}\min\limits_{x \in S} \left( \langle g_k, x \rangle + \frac{1}{\alpha_k}V_{x_k}(x) \right) \\ &= \text{arg}\min\limits_{x \in S} \left(f(x_k)+ \langle g_k, x \rangle + \frac{1}{\alpha_k}V_{x_k}(x) \right) \end{align*}

Здесь левая часть минимизируемого выражения представляет собой аппроксимацию первого порядка, а правая часть представляет собой проекционный член.

2 НАФИГА?

Резонный вопрос, ведь в случае, если мы выбрали \|\cdot\| = \|\cdot\|_2 Евклидову норму и Евклидово расстояние, то этот метод в точности совпадает с тем, что мы уже называем метод проекции субградиента.

Значит, надо предоставить сценарий, когда МЗС работает лучше, давайте рассмотрим S = \Delta_n - вероятностный симплекс, а так же следующее расстояние Брэгмана V_x(y) = \sum_{i \in [n]} y_i \log \frac{y_i}{x_i} = D(y \| x). Норма в прямом пространстве при этом \|\|_1, а в сопряженном - \|\|_\infty. Кроме того, для заданной дивергенции Брэгмана справедливо:

x_0 = \left( 1/n, \ldots, 1/n \right) \; \to \; V_{x_0}(x) \leq \log n \;\;\forall x \in \Delta_n

Тогда алгоритм зеркального спуска запишется в виде:

\begin{align*} x_{k+1} &= \text{arg}\min\limits_{x \in S} \left( \langle \alpha_k g_k, x \rangle + V_{x_k}(x) \right) \\ &= \text{arg}\min\limits_{x \in S} \left( \langle \alpha_k g_k, x \rangle + \sum_{i \in [n]} x_i \log \frac{x_i}{x_{k_i}} \right) \\ &= x_k \cdot \dfrac{e^{-\alpha_k g_k}}{\|x_k \cdot e^{-\alpha_k g_k}\|_1} \end{align*}

А оценки с учетом того, что M = \log n, \|g_k\|_\infty \leq G запишутся, как:

\begin{align*} f(\overline{x}) - f^* \leq \sqrt{\dfrac{2 \log (n) G^2}{T}} \end{align*}

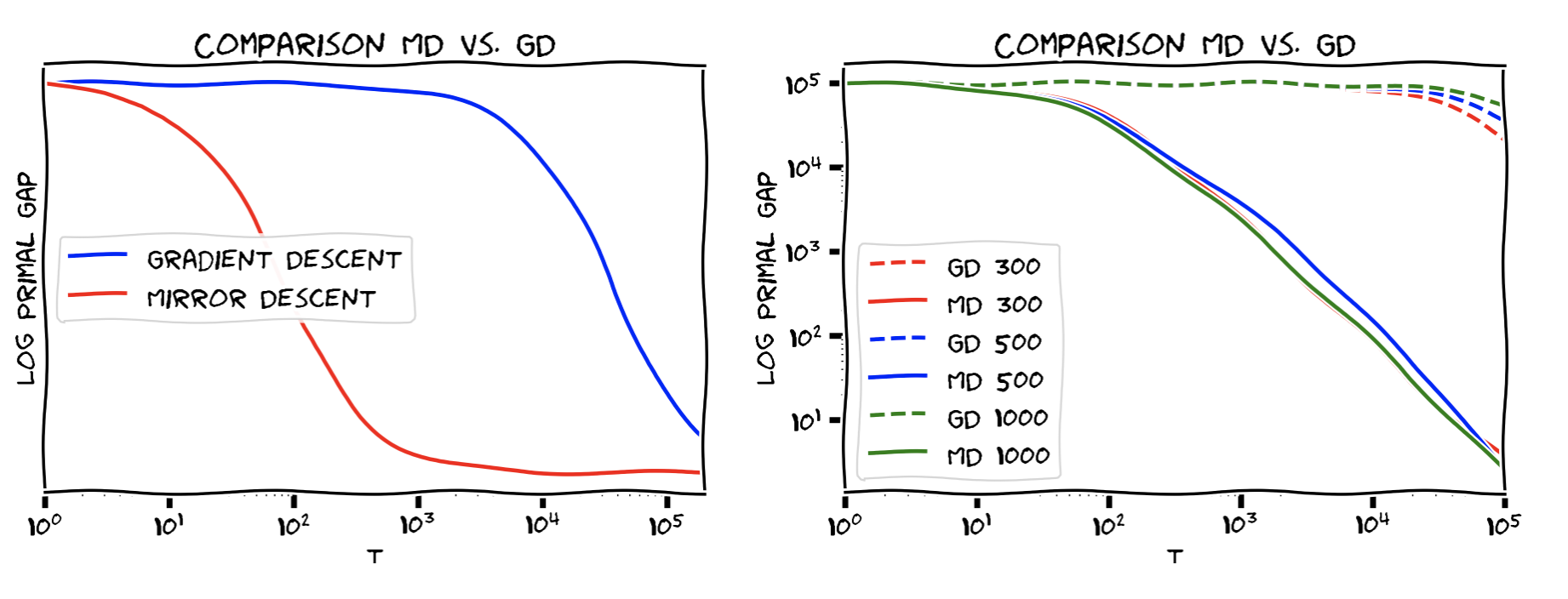
import numpy as np
from matplotlib import pyplot as plt
%matplotlib inline
import seaborn as sns
sns.set()


Ts = np.logspace(0,4, 10)

m = 10
n = 1000
A = np.random.randn(m, n)
x_true = np.random.randn(n)
x_true[x_true < 0] = 0
x_true = x_true/(np.linalg.norm(x_true, 1))

b = A@x_true

x0 = np.ones(n)/n


def f(x):
    return np.linalg.norm(A@x - b, 1)

def grad(x):
    return np.sum(A.T * np.sign(A@x - b), axis=1)

def mirror_descent(x0, grad, T):
    n = len(x0)
    M = np.log(n)
##     G = np.linalg.norm(A,np.inf)*1+np.linalg.norm(b,np.inf)
##     alpha = np.sqrt(2*M/(G**2*T))
    alpha = 0.0001
    xk = x0
    sequence = []
##     print('MD %.3f'%alpha)
    for i in range(int(T)):
        sequence.append(xk)
        g = grad(xk)
        xk = xk * np.exp(-alpha * g) / np.sum(xk * np.exp(-alpha * g))
    return sequence

def projection_subgradient_descent(x0, grad, T):
    n = len(x0)
    M = 0.5
##     G = np.linalg.norm(A,2)*1+np.linalg.norm(b,2)
##     alpha = np.sqrt(2*M/(G**2*T))
    alpha = 0.0001
##     print('GD %.3f'%alpha)
    xk = x0
    sequence = []
    for i in range(int(T)):
        sequence.append(xk)
        g = grad(xk) 
        xk = xk - alpha*g
        xk[xk<0] = 0
        xk = xk/(np.linalg.norm(xk, 1))
    return sequence

result_md = []
result_gd = []

for T in Ts:
    print(T)
    md_T = mirror_descent(x0, grad, T)
    gd_T = projection_subgradient_descent(x0, grad, T)
    
    x_md = np.mean(md_T, axis = 0)
    x_gd = np.mean(gd_T, axis = 0)
    
    result_md.append(f(x_md) - f(x_true))
    result_gd.append(f(x_gd) - f(x_true))

    
plt.loglog(Ts, result_gd, label = 'GD')
plt.loglog(Ts, result_md, label = 'MD')
plt.xlabel('T')
plt.ylabel(r'$f(\overline{x}) - f(x^*)$')
plt.legend()