Neural network Lipschitz constant

1 Lipschitz constant and robustness to a small perturbation

It was observed, that small perturbation in Neural Network input could lead to significant errors, i.e. misclassifications.

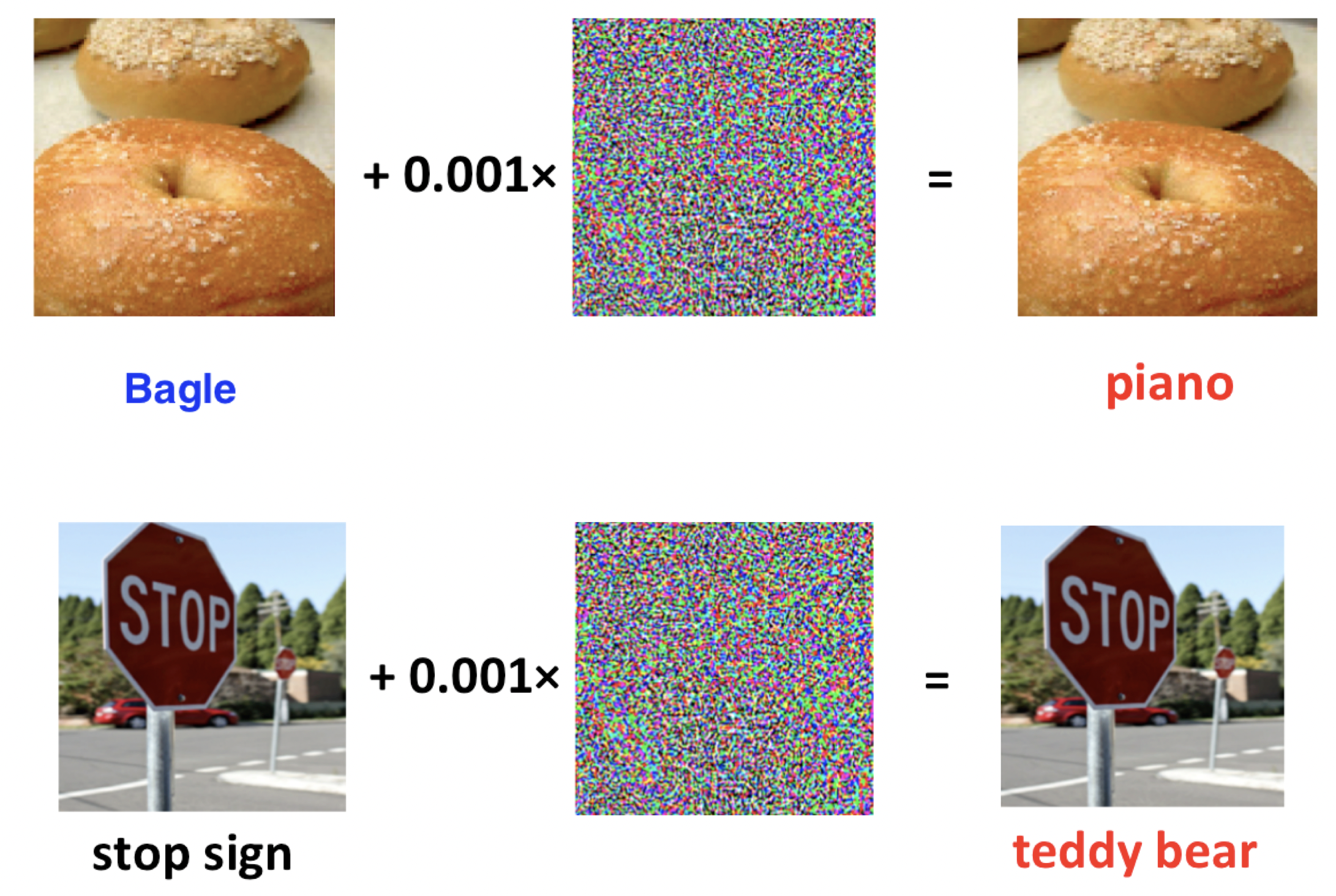
Typical illustration of adversarial attacks in image domain. Source

Lipschitz constant bounds the magnitude of the output of a function, so it cannot change drastically with a slight change in the input

\|\mathcal{NN}(image) - \mathcal{NN}(image+\varepsilon)\| \leq L_{\mathcal{NN}}\|\varepsilon\|

Note, that a variety of feed-forward neural networks could be represented as a series of linear transformations, followed by some nonlinear function (say, \text{ReLU }(x)):

\mathcal{NN}(x) = f_L \circ w_L \circ \ldots \circ f_1 \circ w_1 \circ x,

where L is the number of layers, f_i - non-linear activation function, w_i = W_i x + b_i - linear layer.

2 Estimating Lipschitz constant of a neural network

Theorem

An everywhere differentiable function f: \mathbb{R} \to \mathbb{R} is Lipschitz continuous with L = \sup |\nabla f(x)| if and only if it has bounded first derivative.

Theorem

If f = g_1 \circ g_2, then L_f \leq L_{g_1} L_{g_2}

Therefore, we can bound the Lipschitz constant of a neural network:

L_{\mathcal{NN}} \leq L_{f_1} \ldots L_{f_L} L_{w_1} \ldots L_{w_L}

Example

Let’s consider one the simplest non-liear activation function.

f(x) = \text{ReLU}(x)

Its Lipschitz L_f constant equals to 1, because:

\|f(x) - f(y)\| \leq 1 \|x-y\|

Question

What is the Lipschitz constant of a linear layer of neural network

w(x) = Wx + b

\|w(x) - w(y)\| = \|Wx + b - (Wy + b)\|_2 = \|W(x-y)\|_2 \leq \|W\|_2 \|x-y\|_2 Therefore, L_w = \|W\|_2

3 How to compute \|W\|_2?

Let W = U \Sigma V^T – SVD of the matrix W \in \mathbb{R}^{m \times n}. Then

\|W\|_2 = \sup_{x \ne 0} \frac{\| W x \|_2}{\| x \|_{2}} = \sigma_1(W) = \sqrt{\lambda_\text{max} (W^*W)}

For m = n, computing SVD is \mathcal{O}(n^3).

Time measurements with jax and Google colab CPU.
n 10 100 1000 5000
Time 38.7 µs 3.04 ms 717 ms 1min 21s
Memory for W in fp32 0.4 KB 40 KB 4 MB 95 MB

Works only for small linear layers.

In this notebook we will try to estimate Lipschitz constant of some convolutional layer of a Neural Network.

4 Convolutional layer

Animation of Convolution operation. Source

Suppose, that we have an input X and the convolutional layer C with the filter size k \times k. Here we assume, that p_1, p_2 - are the indices of pixels of the kernel, while q_1, q_2 are the indices of pixels of the output.

C \circ X = \sum_{p_1 = 0}^{k-1}\sum_{p_2 = 0}^{k-1} C_{p_1, p_2} X_{p_1 + q_1, p_2 + q_2}

While multichannel convolution could be written in the following form:

Y_j = \sum_{i = 1}^{m_{in}} C_{:, :, i, j} \circ X_{:, :, i},

where

  • C \in \mathbb{R}^{k \times k \times m_{in} \times m_{out}} – convolution kernel
  • k – filter size
  • m_{in} – number of input channels (e.g., 3 for RGB)
  • m_{out} – number of output channels.

It is easy to see, that the output of the multichannel convolution operation is linear w.r.t. the input X, which actually means, that one can write it as matvec:

\text{vec }(Y) = W \text{vec }(X)

Question

What is the size of the matrix W in this case, if the input image is square of size n?

W \in \mathbb{R}^{m_{out}n^2 \times m_{in}n^2}

Example

If the image size is n = 224, number if input and output channels are m_{in} = m_{out} = 64, then W \in \mathbb{R}^{3 211 264 \times 3 211 264}. Storing this matrix in fp32 requW^T W x_kires approximately 40 Gb of RAM.

It seems, that computing \|W\|_2 is almost impossible, isn’t it?

5 Power method for computing the largest singular value

Since we are interested in the largest singular value and

\|W\|_2 = \sigma_1(W) = \sqrt{\lambda_\text{max} (W^*W)}

we can apply the power method

x_{k+1} = \dfrac{W^T W x_k}{\|W^T W x_k\|_2}

\sigma_{k+1} = \dfrac{W x_{k+1}}{\|x_{k+1}\|_2}

6 Code

Open In Colab{: .btn }

7 References

  • Maxim Rakhuba’s lecture on Matrix and tensor methods in ML.