Binary search

1 Idea

We divide a segment into two equal parts and choose the one that contains the solution of the problem using the values of functions.

2 Algorithm

def binary_search(f, a, b, epsilon):
    c = (a + b) / 2
    while abs(b - a) > epsilon:
        y = (a + c) / 2.0
        if f(y) <= f(c):
            b = c
            c = y
        else:
            z = (b + c) / 2.0
            if f(c) <= f(z):
                a = y
                b = z
            else:
                a = c
                c = z
    return c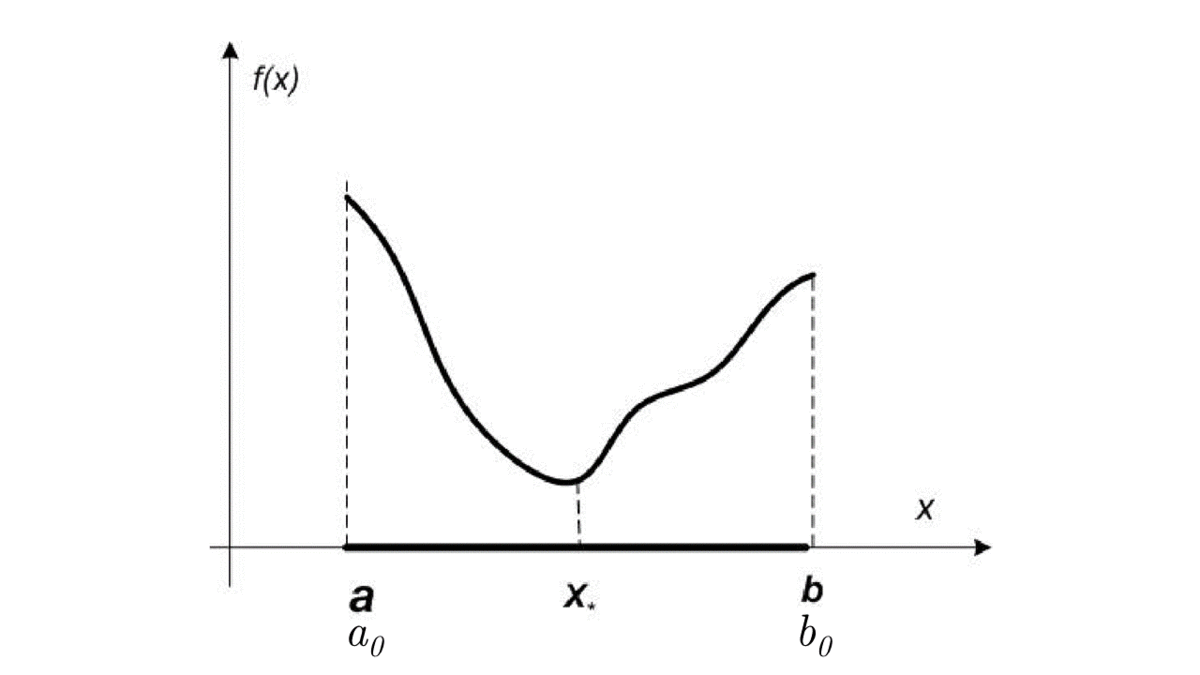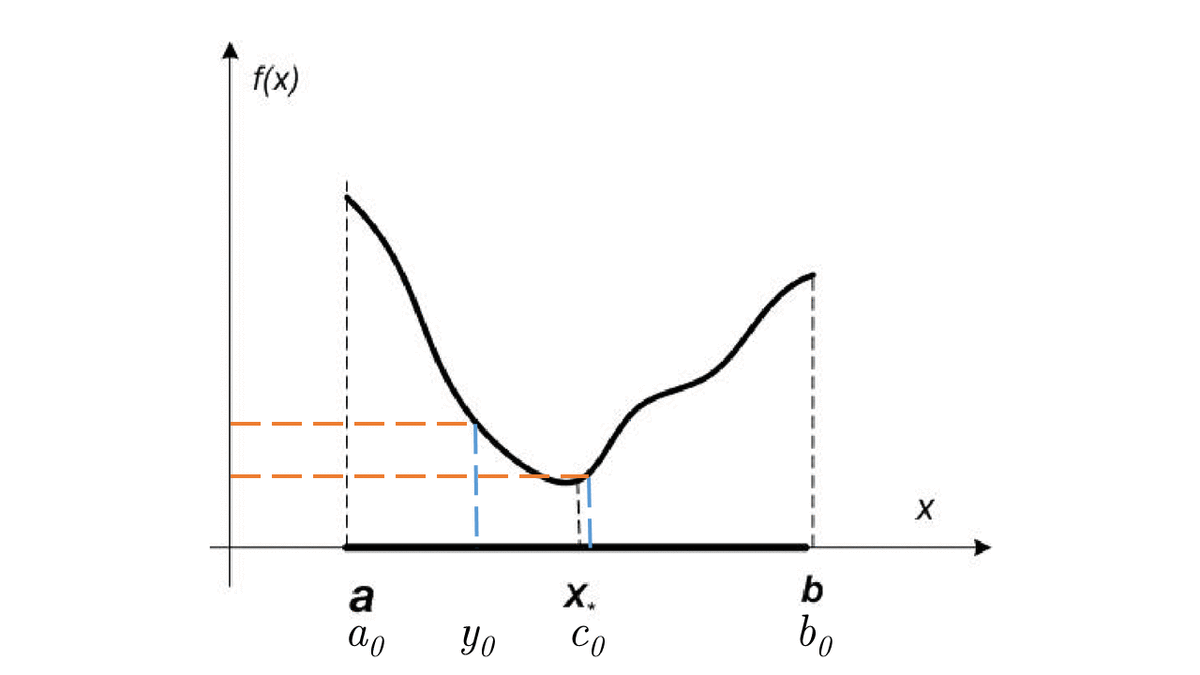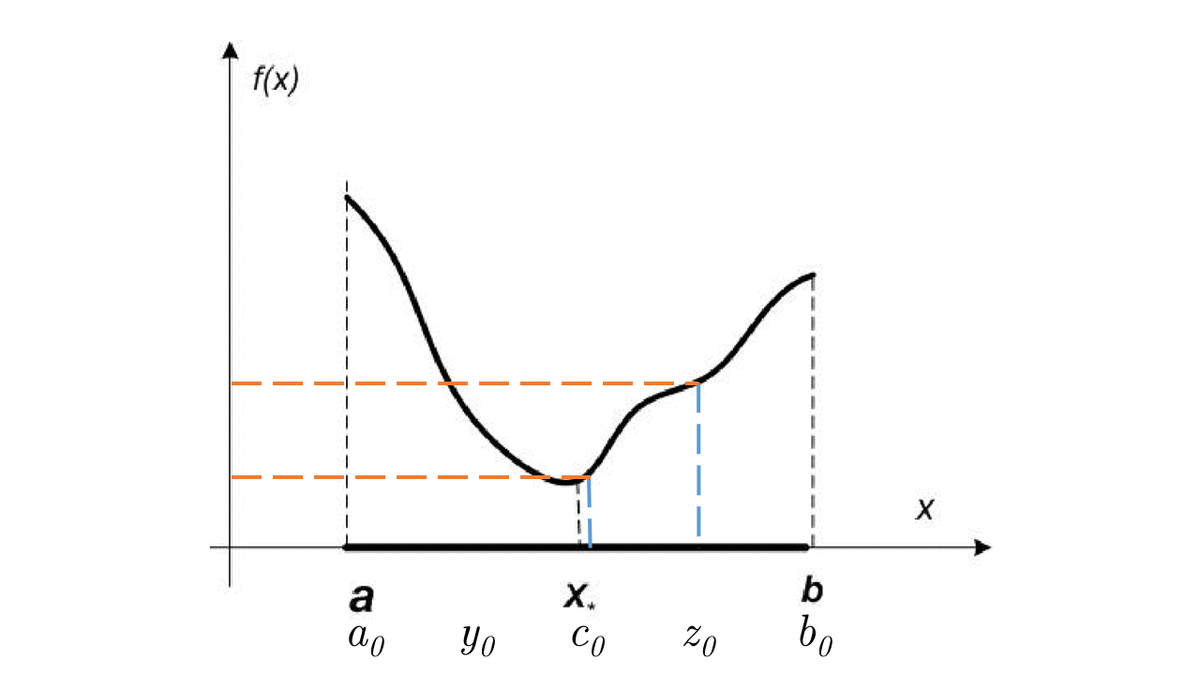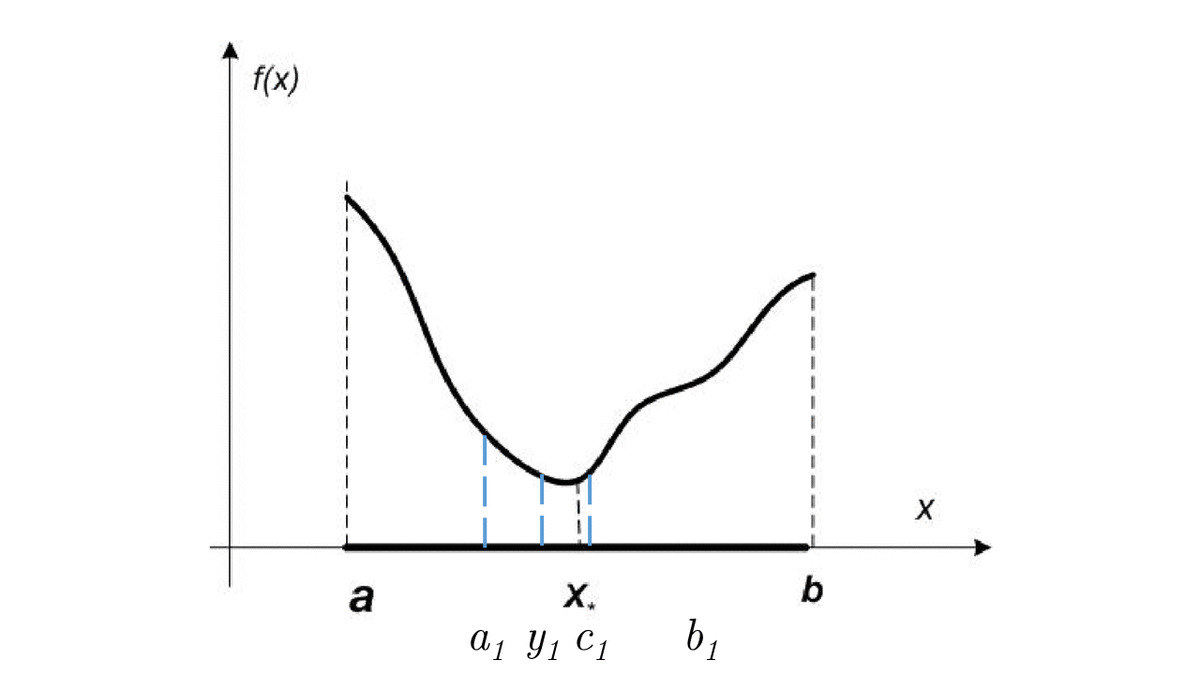

Illustration

3 Bounds

The length of the line segment on k+1-th iteration:

\Delta_{k+1} = b_{k+1} - a_{k+1} = \dfrac{1}{2^k}(b-a)

For unimodal functions, this holds if we select the middle of a segment as an output of the iteration x_{k+1}:

|x_{k+1} - x_*| \leq \dfrac{\Delta_{k+1}}{2} \leq \dfrac{1}{2^{k+1}}(b-a) \leq (0.5)^{k+1} \cdot (b-a)

Note, that at each iteration we ask oracle no more, than 2 times, so the number of function evaluations is N = 2 \cdot k, which implies:

|x_{k+1} - x_*| \leq (0.5)^{\frac{N}{2}+1} \cdot (b-a) \leq (0.707)^{N} \frac{b-a}{2}

By marking the right side of the last inequality for \varepsilon, we get the number of method iterations needed to achieve \varepsilon accuracy:

K = \left\lceil \log_2 \dfrac{b-a}{\varepsilon} - 1 \right\rceil