Travelling salesman problem
1 Problem
Suppose, we have N points in \mathbb{R}^d Euclidian space (for simplicity, we’ll consider and plot case with d=2). Let’s imagine, that these points are nothing else but houses in some 2d village. Salesman should find the shortest way to go through the all houses only once.
That is, very simple formulation, however, implies NP - hard problem with the factorial growth of possible combinations. The goal is to minimize the following cumulative distance:
d = \sum_{i=1}^{N-1} \| x_{y(i+1)} - x_{y(i)}\|_2 \to \min_{y},
where x_k is the k-th point from N and y stands for the N- dimensional vector of indicies, which describes the order of path. Actually, the problem could be formulated as an LP problem, which is easier to solve.
2 🧬Genetic (evolution) algorithm
Our approach is based on the famous global optimization algorithm, known as evolution algorithm. ### Population and individuals Firstly, we need to generate the set of random solutions as an initialization. We will call a set of solutions \{y_k\}_{k=1}^n as population, while each solution is called individual (or creature).
Each creature contains integer numbers 1, \ldots, N, which indicates the order of bypassing all the houses. The creature, that reflects the shortest path length among the others will be used as an output of an algorithm at the current iteration (generation).
2.1 Crossing procedure
Each iteration of the algorithm starts with the crossing (breed) procedure. Formally speaking, we should formulate the mapping, that takes two creature vectors as an input and returns its offspring, which inherits parents properties, while remaining consistent. We will use ordered crossover as such procedure.
2.2 Mutation
In order to give our algorithm some ability to escape local minima, we provide it with mutation procedure. We simply swap some houses in an individual vector. To be more accurate, we define mutation rate (say, 0.05). On the one hand, the higher the rate, the less stable the population is, on the other, the smaller the rate, the more often algorithm gets stuck in the local minima. We choose \text{mutation rate} \cdot n individuals and in each case swap random \text{mutation rate} \cdot N digits.
2.3 Selection
At the end of the iteration we have increased population (due to crossing results), then we just calculate total path distance to each individual and select top n of them.
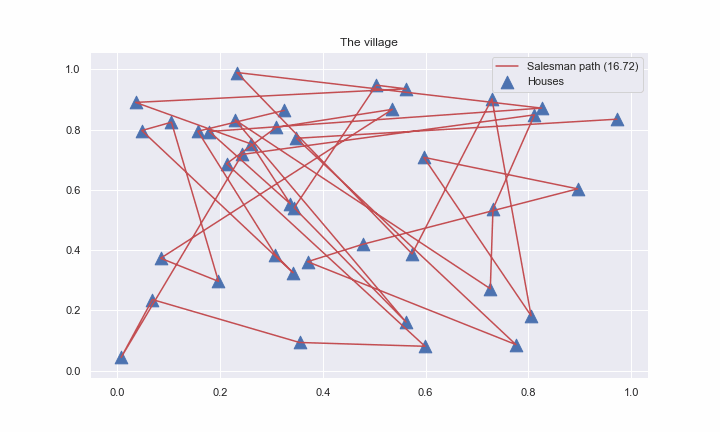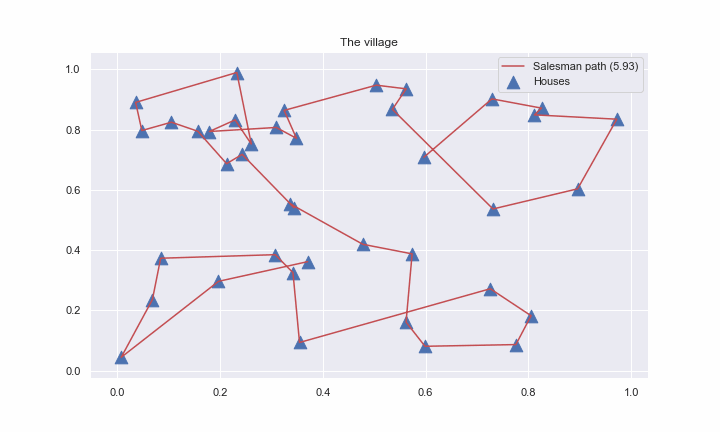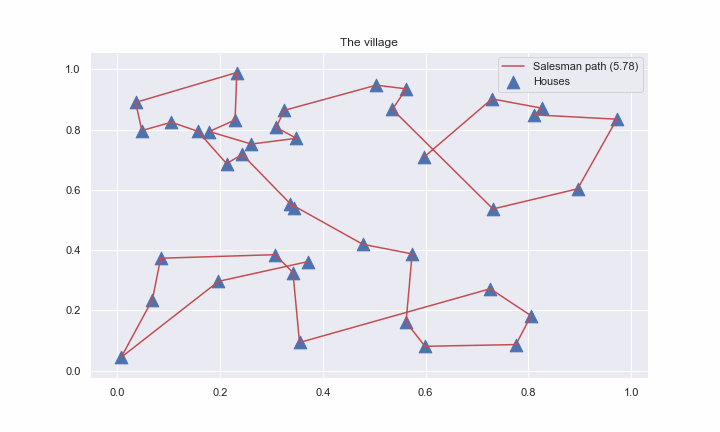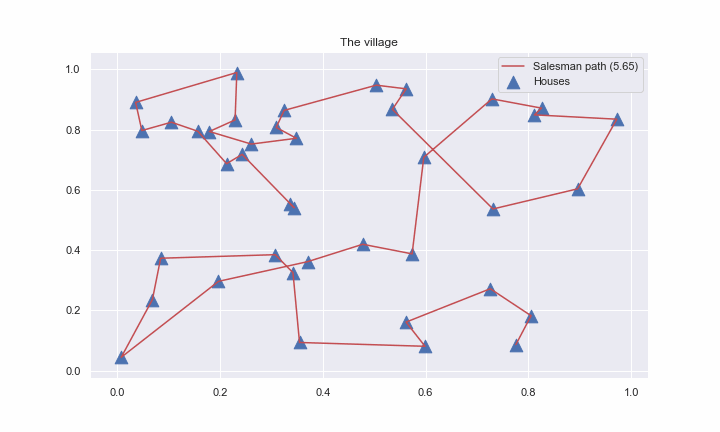
In general, for any c > 0, where d is the number of dimensions in the Euclidean space, there is a polynomial-time algorithm that finds a tour of length at most (1 + \frac{1}{c}) times the optimal for geometric instances of TSP in
\mathcal{O}\left(N(\log N)^{(\mathcal{O}(c{\sqrt {d}}))^{d-1}}\right)